数学オリンピック予選問題（2000年1月10日）

〒160−0022　東京都新宿区新宿6−27−49　協栄生命ビル６Ｆ

TEL 03-5272-9790（通常は月水金の午後）

FAX 03-5272-9791

2000年1月10日 実施

予選問題

受験生への注意事項

試験開始の指示のあるまでこの用紙を開いたり,透かして見たりしてはいけません.

電卓やマイコン,またノートや参考書等を使用してはいけません.

問題は 12問,試験時間は 3時間です.

試験開始後まず,受験番号と氏名と電話番号を解答用紙(別紙)に記入してください.

解答は答のみを解答用紙の該当欄に記入してください.

解答用紙だけを回収します.

問題

†2000年 1月 10日 実施 試験時間 3時間 12問 (答のみを記入する)

１．下図のように 直角三角形内に３つの正方形と３つの円 Ｏ_１，Ｏ_２，Ｏ_３があり、各円はそれぞれを含む小直角三角形の内接円であり、Ｏ_１，Ｏ_３の直径の長さはそれぞれ９，４ である. 円Ｏ_２の直径の長さを求めよ.

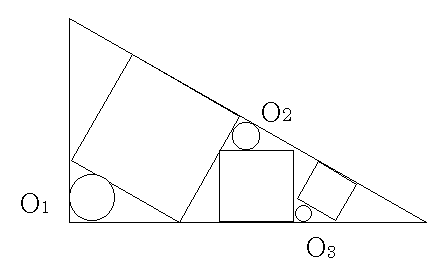
なお, この図は1853年に佐々木 萬蔵が陸奥の国（現在の岩手県）三陸綾里八幡神社に奉納した算額から取ったものである.

２．３ａ＋５ｂ (ただし, a, b は 0 以上の整数) の形で表わせない自然数の最大値を求めよ.

３．平面上に点Oを通る直線ｌ と, 一辺の長さ1 の正三角形OAB がある. ただし, 辺ABとｌは交点を持たないとする. 頂点A, B からｌに下ろした垂線とｌとの交点をそれぞれ A',B' とするとき, AA'+BB' のとりうる最大値を求めよ. ここで2点X,Y に対してXYはその間の距離を示す.

４．一歩で 1段, 2段, または 3段を登れる人が, 7段の石段を登る. 何通りの登り方があるか. ただし途中で下りたり, 足踏みしたりはしないものとする.

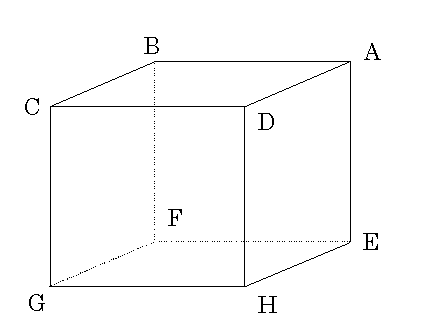
５．図のような1辺の長さ1の立方体ABCD-EFGH があり, 辺CD の中点をK ,辺 DH の中点をL , 辺EF の中点をM ,辺 FB の中点をN とする. 八面体A-KLMN-G の体積を求めよ.

６．n を自然数とする. 有理数係数の2n 次方程式

　 x^{2n}+a₁x^{2n-1}+a₂x^{2n-2}+… +a_2n-1x+a_2n=0

の解は, すべて

　x^2+5x+7=0

の解にもなっている. このとき係数a₁の値を求めよ.

７． 2以上の自然数n に対して,

　　0≦ x ＜ x+y＜ y+z ≦ n

を満たす整数の組 (x,y,z) の総数を求めよ.

８．₄₀Ｃ₂₀を 41 で割った余りを求めよ.

９．∑_k=1¹⁰⁰　( [k^2／100]+[10√k]　)

を求めよ. ただし, [x] はx を超えない最大の整数のことである.

１０．1か2か3の数字が書かれたカードがそれぞれ十分沢山ある. その中からそれぞれの数字のカードを奇数枚ずつ合計1999枚を選び, 一列に並べる. この方法は何通りあるか.

１１．四角形 ABCD があり, AD // BC,∠ ABC＝∠ BDC＝0.5 ∠ ACB であり, 直線 BD は ∠ ABC の2等分線になっているとする. このとき ∠ ABC を求めよ.

１２．数列ａ_１，ａ_２，ａ_３，…，ａ_３０ は以下の条件 (i), (ii) を満たす. このような数列は何通りあるか.

条件

(i)ａ_１，ａ_２，ａ_３，…，ａ_３０は自然数1,2,3,…,30 の並べ換えである.

(ii) mが 2,3,5 のそれぞれの場合, 1 ≦ n ＜n+m ≦ 30 となる任意の n に対して,

a_n+m −a_n は m で割り切れる.

（注）例えば, ａ_１＝１，ａ_２＝２，ａ_３＝３，…，ａ_３０＝３０は条件 (i),(ii) を満たす.

Ｃopyright© 2000 by Mathematical Olympiad Foundation of Japan.

著作権は数学オリンピック財団に帰属します.

HomePageに戻る